 ,
,
то есть последовательность чисел (членов прогрессии), в которой каждое число, начиная со второго, получается из предыдущего добавлением к нему постоянного числа  (шага, или разности прогрессии):
(шага, или разности прогрессии):
 (шага, или разности прогрессии):
(шага, или разности прогрессии):
Любой (n-й) член прогрессии может быть вычислен по формуле общего члена:
Арифметическая прогрессия является монотонной последовательностью . При 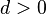 она является возрастающей, а при
она является возрастающей, а при  — убывающей. Если
— убывающей. Если 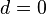 , то последовательность будет стационарной. Эти утверждения следуют из соотношения
, то последовательность будет стационарной. Эти утверждения следуют из соотношения  для членов арифметической прогрессии.
для членов арифметической прогрессии.
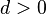 она является возрастающей, а при
она является возрастающей, а при  — убывающей. Если
— убывающей. Если 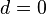 , то последовательность будет стационарной. Эти утверждения следуют из соотношения
, то последовательность будет стационарной. Эти утверждения следуют из соотношения  для членов арифметической прогрессии.
для членов арифметической прогрессии.Общий член арифметической прогрессии
Член арифметической прогрессии с номером  может быть найден по формуле
может быть найден по формуле
 может быть найден по формуле
может быть найден по формуле , где
, где  — первый член прогрессии,
— первый член прогрессии,  — её разность.
— её разность.Характеристическое свойство арифметической прогрессии
Последовательность есть арифметическая прогрессия
есть арифметическая прогрессия  для любого её элемента выполняется условие
для любого её элемента выполняется условие  .
.Сумма первых
 членов арифметической прогрессии
членов арифметической прогрессии- Сумма первых
 членов арифметической прогрессии
членов арифметической прогрессии  может быть найдена по формулам
может быть найдена по формулам , где
, где  — первый член прогрессии,
— первый член прогрессии,  — член с номером
— член с номером  ,
,  — количество суммируемых членов.
— количество суммируемых членов. — формула Алпеева , где
— формула Алпеева , где  — первый член прогрессии,
— первый член прогрессии, 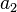 — второй член прогрессии
— второй член прогрессии  — член с номером
— член с номером  .
. , где
, где  — первый член прогрессии,
— первый член прогрессии,  — разность прогрессии,
— разность прогрессии,  — количество суммируемых членов.
— количество суммируемых членов.
Геометри́ческая прогре́ссия — последовательность чисел  (членов прогрессии), в которой каждое последующее число, начиная со второго, получается из предыдущего умножением его на определённое число
(членов прогрессии), в которой каждое последующее число, начиная со второго, получается из предыдущего умножением его на определённое число 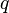 (знаменатель прогрессии), где
(знаменатель прогрессии), где  ,
, 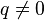 :
: 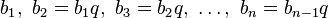 .
.
 (членов прогрессии), в которой каждое последующее число, начиная со второго, получается из предыдущего умножением его на определённое число
(членов прогрессии), в которой каждое последующее число, начиная со второго, получается из предыдущего умножением его на определённое число 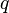 (знаменатель прогрессии), где
(знаменатель прогрессии), где  ,
, 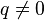 :
: 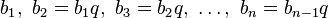 .
.
Любой член геометрической прогрессии может быть вычислен по формуле:
Если  и
и  , прогрессия является возрастающей последовательностью, если
, прогрессия является возрастающей последовательностью, если  , — убывающей последовательностью, а при
, — убывающей последовательностью, а при  — знакочередующейся.
— знакочередующейся.
 и
и  , прогрессия является возрастающей последовательностью, если
, прогрессия является возрастающей последовательностью, если  , — убывающей последовательностью, а при
, — убывающей последовательностью, а при  — знакочередующейся.
— знакочередующейся.
Своё название прогрессия получила по своему характеристическому свойству:
то есть каждый член равен среднему геометрическому его соседей.
- Логарифмы членов геометрической прогрессии (если определены) образуют арифметическую прогрессию.
 , если
, если  .
.- Произведение первых n членов геометрической прогрессии можно рассчитать по формуле:
 .
.- Произведение членов геометрической прогрессии начиная с k-ого члена, и заканчивая n-ым членом, можно рассчитать по формуле:
 .
.- Сумма
 первых членов геометрической прогрессии:
первых членов геометрической прогрессии:

- Если
 , то
, то  при
при  , и
, и
 при
при  .
.
- Сумма
- Произведение членов геометрической прогрессии начиная с k-ого члена, и заканчивая n-ым членом, можно рассчитать по формуле:

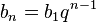

Комментариев нет:
Отправить комментарий